Merge Sort Mastering with Ease: The Most Efficient Sorting Simplified

Merge Sort, a pioneering sorting algorithm, was invented by the eminent mathematician and computer scientist John von Neumann in 1945. Known for his contributions to numerous fields, von Neumann introduced Merge Sort as part of his work on early computer systems, aiming to improve the efficiency of data organization and retrieval. The algorithm’s design leveraged the divide-and-conquer strategy, which involves breaking down a problem into smaller subproblems, solving each subproblem independently, and then combining the solutions to form the final result.

Working Principle of Merge Sort: An Elegant Divide and Conquer Approach

Merge Sort is an efficient, stable, and rather popular algorithm for sorting that applies the divide-and-conquer strategy to set data in order. The crux of the way it works is recursively breaking down the list into smaller sub lists, followed by sorting these sub lists and finally merging them to get a sorted list. In this process, every time the complexity of Merge Sort remains ͑O(n log n) in all the cases, which makes it very efficient for huge data sets.

The divide-and-conquer strategy

1. Divide: Merge Sort initiates the process by splitting the input array into two nearly equal-sized halves. This division is further continued recursively until each subarray has only one element. An array of one element is already sorted and hence forms the base case of this recursion.

2. Conquer: In this phase of the algorithm, the algorithm recursively sorts smaller subarrays. Since each subarray has only one element at the deepest level of recursion, the sorting step at this level is trivial. However, as the recursion unwinds, the algorithm merges these small sorted subarrays into larger sorted subarrays.

3. Merge: This is the step in which actual sorting takes place. Two sorted sub-arrays are taken and merged into one sorted sub-array. It is performed by comparing elements of two sub-arrays and placing the smaller one in the resulting array one at a time, thus keeping the sorted order. The merging process goes on recursively until all the divided sub-arrays become merged into a single sorted array.

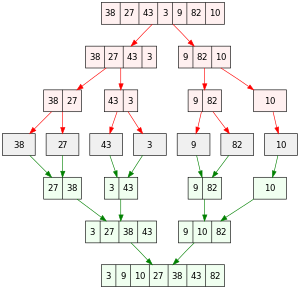
Now, consider this example: an array `A = [38, 27, 43, 3, 9, 82, 10]`. Merge Sort will process it as follows:

1. Divide:

Algorithm for merge sort

Explanation

1. mergeSort Function:

• If the list has one or zero elements, it is already sorted, so return it.
• Otherwise, divide the list into two halves.
• Recursively apply mergeSort to both halves to sort them.
• Merge the two sorted halves into one sorted list using the merge function.

2. merge Function:

• Create an empty list to store the merged result.
• Use two pointers (leftIndex and rightIndex) to track the current positions in the left and right lists.
• Compare the current elements of both lists:
  • If the element in the left list is smaller, add it to the result and move the pointer in the left list forward.
  • Otherwise, add the element from the right list to the result and move the pointer in the right list forward.
• After the comparison loop, if there are remaining elements in either list, add them to the result.
• Return the merged result.

A simple pictorial representation of merge sort

Advantages of Merge Sort: A Detailed Exploration

1. Stable Sorting

Explanation: A sorting algorithm is considered stable when the relative order of equal elements in the input array is maintained           Example: If a list of employees is sorted first by department, then by name, a stable sort will maintain the relative order of employees within the same department.

2. Stable Time Complexity

The time complexity for the working of the Merge Sort algorithm is always O(n log n) Best, average, and worst case scenarios are O(n logn). This independence also makes it reliable for large datasets since performance is always expected to be measured irrespective of the distribution of input data.

3. Parallel Processing

Explanation: This divide-and-conquer approach of Merge Sort lends itself quite naturally to parallel processing. Therefore, a further division of the array into subarrays could be done in parallel. Moreover, a merge process may have its constituents parallelized.  Example of Weather Forecasting : Complex weather models involve dividing the geographical area into grids. Each processor can calculate weather patterns for a specific grid simultaneously. Finally, the individual forecasts are merged to create a comprehensive weather prediction for the entire region. This parallels the divide-and-conquer nature of parallel Merge Sort.

4. Effective for Linked Lists

Explanation: Imagine you have a train of linked boxcars, and you want to sort the boxes by size. Merge sort is a good way to do this because it doesn’t require jumping around the train cause you just cut segments of it.

Here’s why:

• Linked lists don’t have random access: Unlike a regular train where you can easily go to any car, linked lists only let you move from one car to the next. Finding a specific box by jumping around is slow.
• Merge sort works in sections: Merge sort cleverly divides the train in half, sorts each half separately (like sorting two smaller trains), and then merges the sorted halves back together.
• Sorting sections is easier: Sorting smaller sections doesn’t require jumping around as much. You can just compare next-door boxes.
• Merging puts things in order: After sorting the sections, merge sort carefully combines them, making sure the final train is sorted entirely.

Disadvantages of Merge Sort: A Depth Analysis

 1. Space Complexity

• The space complexity for Merge Sort is O(n), where ‘n’ is the size of the input array. This is because the Merge Sort requires extra storage for the temporary arrays used during the merging process.
• Impact: This additional space can be a huge disadvantage when dealing with large data sets or memory-constrained environments. Because of this additional memory overhead, the algorithm can be greatly slowed by high usage of virtual memory due to frequent paging.  

 2. Recursive Overhead

Imagine you have a bunch of folders on your desk, and you want to sort them by name. You can do it one by one, which is like a non-recursive approach. But with a recursive approach, it’s like having a helper friend:

1. Split the folders: You give half the folders to your friend and keep the other half.
2. Friend sorts their half: Your friend sorts their folders by name (recursively, they can keep splitting and sorting if there are many folders).
3. You sort your half: You do the same for your half.
4. Merge the sorted halves: Now you both have sorted sub-piles, and you take turns putting the folders back together, making sure the final pile is completely sorted by name.

This recursive approach is great for merge sort, but there’s a catch:

• Extra work for your friend: Every time your friend helps (recursive call), it takes a little extra effort. They have to remember what folders they’re working on and keep track of things (like a stack of folders to sort).
• Limited desk space: If you have a ton of folders, the stack of things your friend is working on can become too big for your desk (system stack). This can lead to problems like running out of space and not being able to finish sorting (stack overflow error).

 3. Less Efficient for Small Data Sets:

It simply means that the efficiency of any sort of algorithm is inversely proportional to the size of the set input data. Since Merge Sort is usually less efficient for small sets of data as compared to simpler algorithms like Insertion Sort or Bubble Sort, this will mean that when the data set is small, the overhead of making statements for recursion and the merge process outweighs the benefits of performing O(n log n) in complexity.

Practical Applications of Merge Sort

 1. External Sorting in Databases

 Merge Sort has extensive applications in external sorting in databases and file systems. On large datasets that cannot be held in memory, it efficiently deals with data by reading from and writing to external storage, like disk drives. Its sequential access pattern minimizes the number of accesses to the disk; 

 2. Parallel Processing 

Because of its divide-and-conquer approach to problems, Merge Sort can be efficiently parallelized. Each further recursive division of the array into sub-arrays might be done and processed independently in parallel. Similarly, the merge of the sorted sub-arrays can also be parallelized. It has the property that makes it fit for modern multi-core processors and distributed computing environments—and sorting tasks may be divided among many processors or nodes to gain speed in sorting.

Example– Imagine you’re sorting a giant pile of books in a library by title. Merge sort with parallel processing can be visualized like this:

• Divide and Conquer: The librarian splits the pile roughly in half (like the divide step in merge sort).
• Teamwork: Instead of working alone, they call in two strong assistants (multiple processors).
• Parallel Sorting: Each assistant takes half the pile and sorts their books by title independently (like the conquer step happening in parallel). They can spread the books out on separate tables to avoid mixing.
• Merging Expertise: Once each assistant has a sorted sub-pile, the librarian steps in (like the merge step). But here’s the parallel twist:
  • An additional assistant joins (potentially another processor core).
  • The three of them work together, taking turns comparing books from each sorted sub-pile.
  • The librarian (or the designated merging assistant) carefully places the chosen book (based on alphabetical order) into a final sorted pile.
• The Power of Many: By working together like this, the entire team can sort the books much faster than one person could alone. This is the power of parallel processing in merge sort.

 3. Stable Sorting in Applications

 In programs requiring a stable sort—that is, the relative order of elements with equal keys be maintained—Sort is particularly helpful. For instance, in financial applications, Merge Sort allows transactions to be sorted by date and time, but not at the loss of their original order within each date.

Tips for Optimizing Merge Sort Performance

Optimizing the performance of Merge Sort involves various strategies to reduce time complexity, manage memory efficiently, and leverage hardware capabilities. Here are several tips for optimizing Merge Sort performance:

 1. Use Insertion Sort for Small Arrays: Implement Insertion Sort for small subarrays or base cases (e.g., arrays of size ≤ 10). Insertion Sort has lower overhead and constant factor than recursive merges for small arrays, improving overall performance

 2. Optimize Memory Usage: Minimize memory allocation and copying during merging. Efficient memory management reduces overhead and improves cache locality, benefiting performance especially in memory-constrained environments.

Also read Top 10 Best Tools for Data Scientists here.