Insertion sort is one of the simplest and most intuitive sorting algorithms. While it’s challenging to attribute its invention to a single individual, as the algorithm is fundamental and may have been discovered independently by various people, it is generally associated with the early development of computer science and algorithms.
Insertion sort builds a sorted segment of the array or list iteratively. Each element is inserted at its proper position with respect to those already sorted elements. It starts by assuming that the first element is trivially sorted and then compares each element with all the elements in the sorted part. It makes a place for the insertion of an element and shifts the other elements accordingly. The process is done such that the array is always partially sorted.
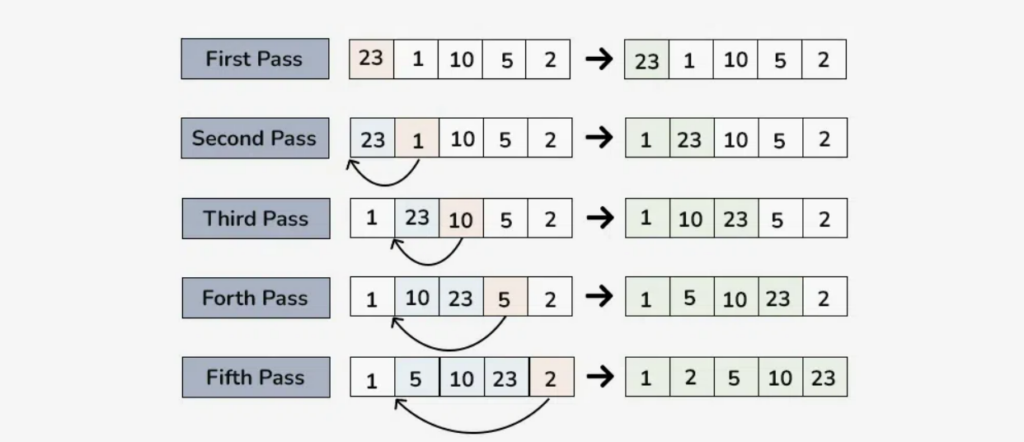
Table of Contents
Working Principle of Insertion Sort
1. Initialization: Start with the assumption that the first element of the array is already sorted.
2. Iterative Sorting: Begin iterating from the second element (index 1) to the end of the array. For each element at position, compare it with the elements to its left (which are part of the sorted segment). Shift elements to the right while the current element is smaller than the elements to its left, to make space for inserting the current element in its correct sorted position.
3. Repeat: By the end of the iteration, the entire array is sorted in ascending order.
Consider sorting the array `[5, 2, 4, 6, 1, 3]` using Insertion Sort:
Start with `[5]` (first element is trivially sorted).
Insert `2` next to `[5]`, resulting in `[2, 5]`.
Insert `4` into `[2, 5]`, resulting in `[2, 4, 5]`.
Insert `6` into `[2, 4, 5]`, resulting in `[2, 4, 5, 6]`.
Insert `1` into `[2, 4, 5, 6]`, resulting in `[1, 2, 4, 5, 6]`.
Insert `3` into `[1, 2, 4, 5, 6]`, resulting in `[1, 2, 3, 4, 5, 6]`.
A pseudo-code algorithm
Summary of the Steps for Insertion Sort
- Initial List: Start with the list [38, 27, 43, 3, 9, 82, 10].
- First Pass: Compare 27 with 38, insert 27 before 38.
- Second Pass: 43 is already in the correct position.
- Third Pass: Compare 3 with 43, 38, and 27, and insert 3 before 27.
- Fourth Pass: Compare 9 with 43, 38, 27, and 3, and insert 9 before 27.
- Fifth Pass: 82 is already in the correct position.
- Sixth Pass: Compare 10 with 82, 43, 38, 27, 9, and 3, and insert 10 before 27.
- Best Case: (O(n)) when the array is already sorted.
- Worst Case: (O(n^2)) when the array is in reverse order or nearly sorted in reverse.
- Average Case: (O(n^2))
Space Complexity: (O(1)) additional space, making it an in-place sorting algorithm.
Insertion Sort’s performance can vary significantly based on the initial order of the elements. It performs efficiently on small datasets or when the array is already partially sorted, but may become inefficient for larger datasets due to its quadratic time complexity.
Advantages of Insertion Sort: Efficiency and Practicality
1. Efficient on Small Datasets: It performs efficiently on small datasets or arrays that are nearly sorted. Insertion sort can get close to linear complexity in time, especially in the best case when the array is already sorted.
2. In-Place Sorting: Insertion sort performs the task of sorting an array in place, using additional memory space of only constant size. This might be pretty handy in low-resource memory systems or embedded systems with limited available memory for allocation.
3. Adaptive: Insertion sort is adaptive, meaning it works powerfully with input arrays already partially sorted—that is, the number of comparisons and shifts to sort the array is minimized, especially if the elements are already in sorted order.
4. Stable sorting: Insertion sort is a stable sorting algorithm, which implies that the relative order of equal elements in the array after sorting is retained. This is valuable in many applications. For example, sorting something with the orders of date and time.
5. Online Algorithm: Insertion sort can handle an array while it is arriving—one element at a time. That can be very useful when the input is streaming or is coming in real-time and needs to be continuously sorted without keeping the elements in the memory.
Disadvantages of Insertion Sort: Considerations and Limitations
1. Quadratic Time Complexity: Insertion Sort has a time complexity of (O(n^2)) in the worst-case scenario. This occurs when the array is sorted in reverse order or nearly sorted in reverse, leading to a large number of comparisons and shifts.
2. Inefficient for Large Datasets: Due to its quadratic time complexity, Insertion Sort becomes inefficient for sorting large datasets. Sorting (n) elements using Insertion Sort may require (n^2) operations in the worst case, making it impractical for applications that involve sorting large amounts of data quickly.
3. Space Complexity: While Insertion Sort has (O(1)) additional space complexity (in-place sorting), it may not be optimal in terms of memory usage for large datasets. In-place sorting algorithms like Quicksort or Heapsort can achieve (O(log n)) space complexity due to their recursive nature or additional data structures, making them more memory-efficient for sorting larger arrays.
4. Not Suitable for Parallelization: Insertion Sort is inherently sequential and does not lend itself well to parallelization. Sorting tasks cannot easily be divided among multiple processors or threads, limiting opportunities for performance optimization in multi-core or distributed computing environments.
Practical Applications of Insertion Sort
1. Online Algorithms: Insertion Sort can sort data as it receives it, making it suitable for applications with streaming or real-time data. Example: Sorting incoming data in an online trading system where transactions are processed in real-time and need to be quickly ranked or sorted.
2. Auto-complete and Spell Check Systems: As users type, words are added to the dictionary and need to be placed in the correct order. Insertion sort can efficiently handle this by inserting new words into their appropriate positions in an already sorted list.
3. Embedded Systems: Insertion Sort’s simplicity and minimal memory usage make it suitable for sorting operations in resource-constrained environments. Example: Sorting sensor data in embedded devices where memory and computational resources are limited, such as in IoT devices or microcontrollers.
Tips for Optimizing Insertion Sort Performance
- Early Exit for Sorted Arrays: Add a check to detect if the array is already sorted, allowing the algorithm to exit early if no swaps are made in a pass.
- Minimize Swaps with Binary Search: Use binary search to find the correct position of the element to be inserted. This reduces the number of comparisons needed to find the insertion point from O(n)O(n)O(n) to O(logn)O(\log n)O(logn).
- Optimized Inner Loop: Instead of shifting elements one by one, shift blocks of elements where possible. This can be done by keeping track of the largest sorted section and moving it as a block.
- hybrid Algorithms: For larger datasets, combine insertion sort with a more efficient sorting algorithm like merge sort or quicksort. This approach uses insertion sort for smaller subarrays within the larger sorting algorithm, capitalizing on its efficiency with small datasets.
- Parallel Processing: Although insertion sort is inherently sequential, for very large datasets, consider dividing the data into smaller chunks, sorting them in parallel using insertion sort, and then merging the results. This approach can leverage multi-core processors to improve performance.
Also read Top 10 Best Tools for Data Scientists here.